This chapter introduces a useful technique called stratification, which is the process of splitting a finite population into subgroups and then taking independent samples from each of those subgroups. The sampling within strata may be a simple random sample, or another design such as cluster sampling. We will however concentrate on the case of simple random sampling as the within-stratum sampling scheme.
Stratification is an example of using auxiliary information about the population at the design stage. This information is used to put each unit into one of the strata.
There are several reasons for stratification. Some of these are:
We will briefly look at 1 and 2. In which case when we form strata we are trying to form subgroups of the population which are more homogeneous than the total population. One measure of homogeneity is the CV (coefficient of variation: \(S_Y/\bar\) ) of the variable, and so we try to form subgroups whose CV’s are much less than the population CV’s.
Example. \(N=1000\) students enrol in a first year statistics course. We are given a list of their names, and for each person we are also told whether or not they have a degree: 100 do have a degree already and 900 do not. We are asked to estimate the mean age of students in the class, and we are only allowed to sample 20 students.
How should we proceed?
We could take a simple random sample of students, and calculate the mean age \(\bar\) of the sample, and use that as our estimate. However it’s very likely that the people who already have degrees are older, and moreover the spread of ages in that group is likely to be much wider than in the no degree group. It would therefore make sense to take two separate samples, one from each group, separately estimate the mean of each group, and then combine those estimates to form the overall mean estimate. This is called stratified sampling, and it can lead to estimates which are much more precise than those from simple random sampling.
In stratified sampling we require prior information on every unit in the population (not just the sampled units). We use this prior auxiliary information to classify every population unit into one, and only one stratum. We’ll leave the method of deciding how to form the strata for later.
For the moment suppose that we have determined our strata, and there are \(H\) of them. The \(N\) population units are divided up with \(N_h\) units in each stratum: \[\begin N = \sum_^H N_h \end\] Every population unit belongs to one and only one stratum \(h\) . The proportion of the population in stratum \(h\) is \(F_h\) \[\begin F_h = \frac \qquad \text \qquad \sum_^H F_h = 1 \end\]
Example continued. Our class of \(N=1000\) students can be split into \(H=2\) strata – those without and those with degrees:
| \(h\) | Stratum | Stratum Size | Stratum Proportion |
|---|---|---|---|
| 1 | No degree | \(N_1=900\) | \(F_1=\frac=\frac=0.9\) |
| 2 | Has degree | \(N_2=100\) | \(F_2=\frac=\frac=0.1\) |
| Total | \(N=\sum_hN_h=1000\) | \(\sum_hF_h=1.0\) |
We relabel each unit by its stratum \(h\) and unit number \(i\) within that stratum. So the within stratum total for stratum \(h\) is the sum of all the \(Y\) values for units in stratum \(h\) : \[\begin Y_h = \sum_^ Y_ \end\] similarly we have the within stratrum mean and variance: \[\begin \bar_h &=& \frac \sum_^ Y_ = \frac\\ S_h^2 &=& \frac \sum_^ (Y_-\bar_h)^2 \end\] These formulae are identical to those we have had before, only we have the label \(h\) to show that they are being calculated separately in each stratum.
Example continued. Our class of \(N=1000\) students can be split into \(H=2\) strata – those without and those with degrees:
| \(h\) | Stratum | Stratum Total | Stratum Mean | Stratum Variance |
|---|---|---|---|---|
| 1 | No degree | \(Y_1=18435.6\) | \(\bar_1=20.5\) | \(S_1^2=2.08\) |
| 2 | Has degree | \(Y_2=3161.6\) | \(\bar_2=31.6\) | \(S_2^2=50.03\) |
| Total | \(Y=\sum_hY_h=21597.2\) |
The overall population total is simply the sum of all the within stratum totals: \[\begin Y = \sum_^H Y_h \tag \end\] However we have to be careful when combining the within stratum results to form the overall population mean and variance. The population mean is given by \[\begin \bar &=& \frac\\ &=& \frac<\sum_^ Y_h>\\ \tag &=& \frac<\sum_^ N_h\bar_h>\\ &=& \sum_^ \frac\bar_h\\ &=& \sum_^ F_h \bar_h \end\] i.e. the population mean is a weighted sum of the stratum means \(Y_h\) .
Example continued. To find the mean age of the 1000 students, form the weighted sum: \[ \bar = \sum_^ F_h \bar_h = (0.9)(20.5) + (0.1)(31.6) = 21.6 \]
Example continued. To find the variance of the ages of the 1000 students, form the two components:
\[\begin \text &=& \frac\sum_^H (N_h-1) S_h^2\\ &=& \frac = \frac = 6.83\\ \text &=& \frac\sum_^H N_h (\bar_h-\bar)^2\\ &=& \frac<(900)(20.5-21.6)^2)+(100)(31.6-21.6)^2> = \frac = 11.10\\ \text &=& S_Y^2 = \frac\sum_^H (N_h-1) S_h^2 + \frac\sum_^H N_h (\bar_h-\bar)^2\\ &=& 6.83 + 11.10 = 17.93 \end\]
The total variance has been partitioned into two parts by the stratification – most of the total variance is between the strata, which is highly desirable.
The power of stratification lies in the separation of between and witin stratum variance. All our sampling error comes from the within stratum variances \(S_h^2\) , so if we can push as much of \(S_Y^2\) into the between stratum variance, we won’t see that variance in our estimators and they will be much more accurate.
The key concept in stratified sampling is that we have divided the population into \(H\) groups, and we take completely independent samples from each stratum: it’s as if we were running \(H\) separate surveys.
This means that the sampling method can be different in each stratum: we could take a SRS in one stratum, a census in another, a cluster sample in another etc.
Then the natural estimator for the population total is \[\begin \estm_ = \sum_^ \estm_h \end\] where \(\estm_h\) is an estimator (appropriate to the sampling scheme) for the total for stratum \(h\) . The variance of this estimator is easy to work out since the sampling is independent in each stratum. \[\begin \bfa<\estm_> = \sum_^ \bfa<\estm_h> \end\] where \(\bfa<\estm_h>\) is the variance of the estimator for the total for stratum \(h\) .
The natural estimator of the population mean is: \[\begin \estm>_ &=& \frac_>\\ &=& \frac \sum_^ \estm_h\\ &=& \frac \sum_^ N_h\estm>_h\\ &=& \sum_^ F_h\estm>_h \end\] and its variance is \[\begin \bfa<\estm>_> = \sum_^ F_h^2 \bfa<\estm>_h> \end\] This is a weighted sum of the variances of the stratum mean estimates, just as the mean was a weighted sum of the stratum means, but note that \(F_h\) appears as \(F_h^2\) .
To take a specific example of a sampling scheme, suppose that we take a SRS of size \(n_h\) from each stratum and these samples are independent. Then the within stratum estimates of totals, means and proportions are: \[\begin \nonumber \estm_h &=& \frac \sum_^ y_ = N_h\bar_h\\ \estm<\bar>_h &=& \frac \sum_^ y_ = \bar_h\\ \nonumber \estm
_h &=& \frac \sum_^ y_ = \bar_h \end\] with variances \[\begin \nonumber \bfa<\estm_h> &=& N_h^2\left(1-\frac\right)\frac\\ \bfa<\estm<\bar>_h> &=& \left(1-\frac\right)\frac\\ \nonumber \bfa_h> &=& \left(1-\frac\right)\frac \end\] which can be estimated from sample data by: \[\begin \nonumber \bfa<\widehat><\estm_h> &=& N_h^2\left(1-\frac\right)\frac\\ \bfa<\widehat><\estm<\bar>_h> &=& \left(1-\frac\right)\frac\\ \nonumber \bfa<\widehat>_h> &=& \left(1-\frac\right)\frac_h(1-\estm
_h)> \end\] These formulae are identical to the SRS formulae we have had earlier, with the single change that we have a subscript \(h\) to indicate that the estimates and variances are specific to stratum \(h\) .
Example continued. Assume we have drawn a sample of size 10 from each of the two strata. The sample statistics are as given in the following table:
| Stratum | Stratum Size | Stratum Fraction | Sample Size | Sampling Fraction | Sample Weight | Sample Mean Age | Sample Variance | |
|---|---|---|---|---|---|---|---|---|
| \(h\) | \(N_h\) | \(F_h=\frac\) | \(n_h\) | \(f_h=\frac\) | \(w_\) | \(\bar_h\) | \(s_h^2\) | |
| 1 | No degree | 900 | 0.9 | 10 | 0.0111 | 90 | 20.3 | 3.22 |
| 2 | Has degree | 100 | 0.1 | 10 | 0.1000 | 10 | 37.8 | 56.2 |
| Total | 1000 | 1.0 | 20 |
Note that the sampling fractions and hence the sample weights are different in the two strata.
Using these data we can estimate the mean age in each stratum, and create a 95% confidence interval for each estimate:
| Stratum | Estimated Mean Age | Variance of Estimate | Std. Error of Estimate | RSE | 95% Conf. Int. | |
|---|---|---|---|---|---|---|
| \(h\) | \(\estm>_h=\bar_h\) | \(\bfa<\estm>_h>\) | \(\bfa<\estm>_h>\) | \(\bfa<\estm>_h>\) | ||
| 1 | No degree | 20.3 | 0.3181 | 0.56 | 0.028 | (19.2, 21.4) |
| 2 | Has degree | 37.8 | 5.0573 | 2.25 | 0.060 | (33.4, 42.2) |
Example continued. An overall estimate of the mean age of the \(N=1000\) students from the sample is given by \[ \estm> = \sum_^H F_h\bar_h = (0.9)(20.3) + (0.1)(37.8) = 22.1 \] with variance \[\begin \bfa><\estm>> &=& \sum_^ F_h^2 \left(1-\frac\right)\frac\\ &=& (0.9)^2\left(1-\frac\right)\frac +(0.1)^2\left(1-\frac\right)\frac = 0.3085 \end\] leading to the following 95% confidence interval for the mean student age in the whole class of 1000 students: \[ 22.1 \pm (1.96)\sqrt = 22.1\pm1.1 = (21.0,23.2) \]
Example continued. Now assume that in the example above we had asked about car ownership, and found that 3 of the sampled students without degrees owned a car, whereas there were 8 car owners among those with degrees. What is the proportion of car owners in the whole population?
First compute the proportions in the two strata: \[\begin \widehat
_1 &=& \frac = 0.30\\ \widehat
_2 &=& \frac = 0.80 \end\] Then combine these estimates to form the full population estimate: \[ \widehat
= \sum_hF_h\widehat
_h = (0.9)(0.30) + (0.1)(0.80) = 0.35 \] with variance \[\begin \bfa> &=& \sum_h F_h^2\left(1-\frac\right) \frac_h(1-\widehat
_h)>\\ &=& (0.9)^2\left(1-\frac\right)\frac +(0.1)^2\left(1-\frac\right)\frac = 0.01885 \end\] leading to the following 95% confidence interval for the proportion of car owners in the whole class of 1000 students: \[ 0.35 \pm (1.96)\sqrt = 0.35\pm 0.27 = (0.08,0.62) \] Scaling these estimates by the population size \(N=1000\) gives an estimate of the total number of car owners \[ \widehat = N\widehat
= (1000)(0.35) = 350 \] with 95% confidence interval \[ N\times(0.08,0.62) = 1000\times(0.08,0.62) = (80,620) \]
When we evaluate a sampling scheme, our main concern is usually to see whether it results in improved or worsened estimates than those obtainable under other sampling schemes. By improved we usually mean estimates with a smaller sampling error, although other factors such as cost and the need to form good subpopulation estimates may be important as well.
The standard comparison we make is to compare the variance of an estimator \(\estm_\text\) under the proposed complex sampling scheme, with the variance of the equivalent estimator under simple random sampling \(\estm_\text\) with the same sample size. This comparison is made by forming the design effect – which is the ratio of the two variances: \[\begin \bfa<\estm_\text> = \frac<\estm_\text>><\estm_\text>> \tag \end\] If the Deff is greater than 1, then the variance of \(\estm_\) is greater than that of the SRS estimator \(\estm_\) . The estimator \(\estm_\) is then said to be less efficient than \(\estm_\) . A desirable Deff is therefore less than one, indicating that the complex design is more efficient.
Example continued. We want to know if the stratified estimator of the mean student age is an improvement over simple random sampling. For \(n=20\) the SRS estimator of the mean has variance \[ \bfa>_> = \left(1-\frac\right)\frac = \left(1-\frac\right)\frac = 0.8786 \] For a stratified sample of \(n=20\) allocated with 10 units in each stratum \[\begin \bfa>_> &=& \sum_^H F_h^2\left(1-\frac\right)\frac\\ &=& (0.9)^2\left(1-\frac\right)\frac + (0.1)^2\left(1-\frac\right)\frac = 0.2117 \end\] so the design effect is \[ \bfa>_> = \frac<\bfa>_>><\bfa>_>> = \frac = 0.24 \] This is less than one, showing that the stratified estimator (for this allocation of a sample of size \(n=20\) ) is more efficient.
In general \(S_Y^2\) and \(S_h^2\) , which are required in the formula for the Deff, are unknown and must be estimated using sample data. The within stratum variances \(S_h^2\) are simply estimated by the corresponding sample variances \(s_h^2\) , however the overall population variance is a little more complex. From Equation (8.3) we had \[ S_Y^2 = \frac\left( \sum_^H (N_h-1) S_h^2 +\sum_^H N_h (\bar_h-\bar)^2\right) \] and it follows that an estimate of \(S_Y^2\) is given by \[\begin \estm_Y^2 = \sum_^H F_h s_h^2 + \sum_^H F_h(\bar_h-\estm<\bar>_)^2 \ \ \ \text\ \ \ \estm<\bar>_ = \sum_^H F_h\bar_h \end\] > = ^H F_h_h \end So to calculate the Deff of the estimator of the mean from sample data in stratified SRSWOR we calculate \[\begin \bfa><\estm<\bar>_> &=& \sum_^H F_h^2\left(1-\frac\right)\frac\\ \bfa><\estm<\bar>_> &=& \left(1-\frac\right)\frac \left[ \sum_^H F_hs_h^2 + \sum_^H F_h (\bar_h-\estm<\bar>_)^2 \right] \end\] and then compute \[ \bfa><\estm<\bar>_> = \frac<\bfa><\estm<\bar>_>>< \bfa><\estm<\bar>_>> \] Note: to get a good estimate of the variance of the estimator and its Design Effect we need sufficient sample size in each stratum to get reliable estimates of \(\bar_h\) and \(s_h^2\) . Small samples lead to very unreliable estimates of variances in general.
Example continued. We have already estimated \(\bfa>>_>=0.3085\) from the sample. It remains to estimate \(\bfa>>_>\) : \[\begin \bfa>>_> &=& \left(1-\frac\right)\frac \left[ \sum_^H F_hs_h^2 + \sum_^H F_h (\bar_h-\estm>_)^2 \right]\\ &=& \left(1-\frac\right)\frac [ (0.9)(3.22)+(0.1)(56.2) \\ && \qquad\qquad +(0.9)(20.3-22.1)^2+(0.1)(37.8-22.1)^2 ]\\ &=& (0.049)[8.518+27.565] = 1.7681 \end\] leading to an estimate of the Deff of \[ \bfa>>_> = \frac<\bfa>>_>>< \bfa>>_>> = \frac = 0.17 \] which is similar to the true value of 0.24, and likewise indicates that the stratified design is much more efficient than SRSWOR.
The Deff can be used in two important ways:
If the Deff is less than 1, the complex design requires a smaller sample size for the same accuracy, OR achieves lower margin of error for the same sample size. i.e. the complex design is better. If the Deff is greater than 1, the SRS is better than the complex design.
In general the Design Effect is the ratio of the variance of an estimator under some complex design (such as stratified sampling), to the variance of an estimator under SRSWOR, with the same sample size: \[\begin \bfa> = \frac_>>_>> \end\]
Now assume we have a sample of size \(n_1\) in the complex design, and a sample of size \(n_2\) in a SRSWOR, and we have chosen \(n_2\) so that the variances of the two estimators are equal: \[ \bfa>_>_ = \bfa>_>_ \] then the Deff becomes simply \[\begin \bfa>_>_ = \frac \end\] Thus if it takes a sample of size \(n_\) to achieve a certain accuracy under SRSWOR, then it will take a sample of size \[\begin n_ = n_\times \bfa>_> \end\] to achieve the same precision under the complex design.
Example. For a variable with a Design Effect of 0.2 what size sample is required to achieve the same accuracy as a SRSWOR with \(n_=500\) ? \[ n_ = 0.2\times500 = 100 \] Only a sample of size 100.
The Design Effect thus tells us by what factor our sample size is reduced (or increased) by the use of the complex design.
We can also use the design effect to see the effect of a design on confidence intervals. The SRS 95% confidence interval is \[ \widehat_ \pm 1.96\times \bfa<\widehat_> \] Using the Deff the variance and standard error of \(\estm_\) are \[ \begin \bfa<\widehat_> &= \bfa<\widehat_> \bfa<\widehat_>\\ \bfa<\widehat_> &= \sqrt<\bfa<\widehat_>> \bfa<\widehat_>\\ \end \] then under the complex design the equivalent 95% confidence interval \[ \widehat_ \pm 1.96\times \bfa<\widehat_> \] can be written \[ \widehat_ \pm 1.96\times \sqrt<\bfa<\widehat_>>\bfa<\widehat_> \]
The weight of sample member \(k\) in stratum \(h\) of a stratified simple random sample is \[ w_ = \frac \] Estimates of totals in stratified SRSWOR are formed just as they are in SRS, but the weights can differ between sample members due to the differing sample fractions in each of the strata.
The goal of stratification is to put units which are similar to each other, but different from the rest of the population, all together in a single stratum.
If a stratum contains a lot of highly unusual and influential units then we sample from that stratum with high probability, and consequently give each sample member from that stratum a low weight. A good example of this is in buiness surveys where a small number of big companies can dominate estimates of total revenues in certain sectors of the economy. Such companies are usually grouped together into a single stratum, and a census is taken in that stratum.
Given a survey population of size \(N\) form a stratified sample of size \(n\) by the following steps.
We have some auxiliary variable \(X_i\) which we believe is correlated with the variable of interest \(Y_i\) . We have a (measured or estimated) value of \(X_i\) for every unit in the population: this may have come from some previous survey or census.
How can we use this information to form strata?
One way of producing homogeneous strata is the cumulative \(\sqrt\) rule>: The rule is to form stratum boundaries so that the intervals are equal on the cumulative \(\sqrt\) scale. This requires carrying out the following steps:
i.e. divide the total cumulative \(\sqrt\) by \(H\) , call this \(I=\frac\sum_^\sqrt\) and consider the \(H-1\) numbers \(I,\; 2\times I, \; \ldots, \; \left(H-1\right) \times I\)
For each of these numbers \(h\times I\) , look for the histogram bin whose cumulative \(\sqrt\) is closest to \(h\times I\) and then the stratum boundary is the right hand end of that histogram bin. (Clearly 0 and the population size are also boundaries.)
This method is an approximation which can be done with hand calculations and say a published table showing the frequencies distribution in certain intervals.
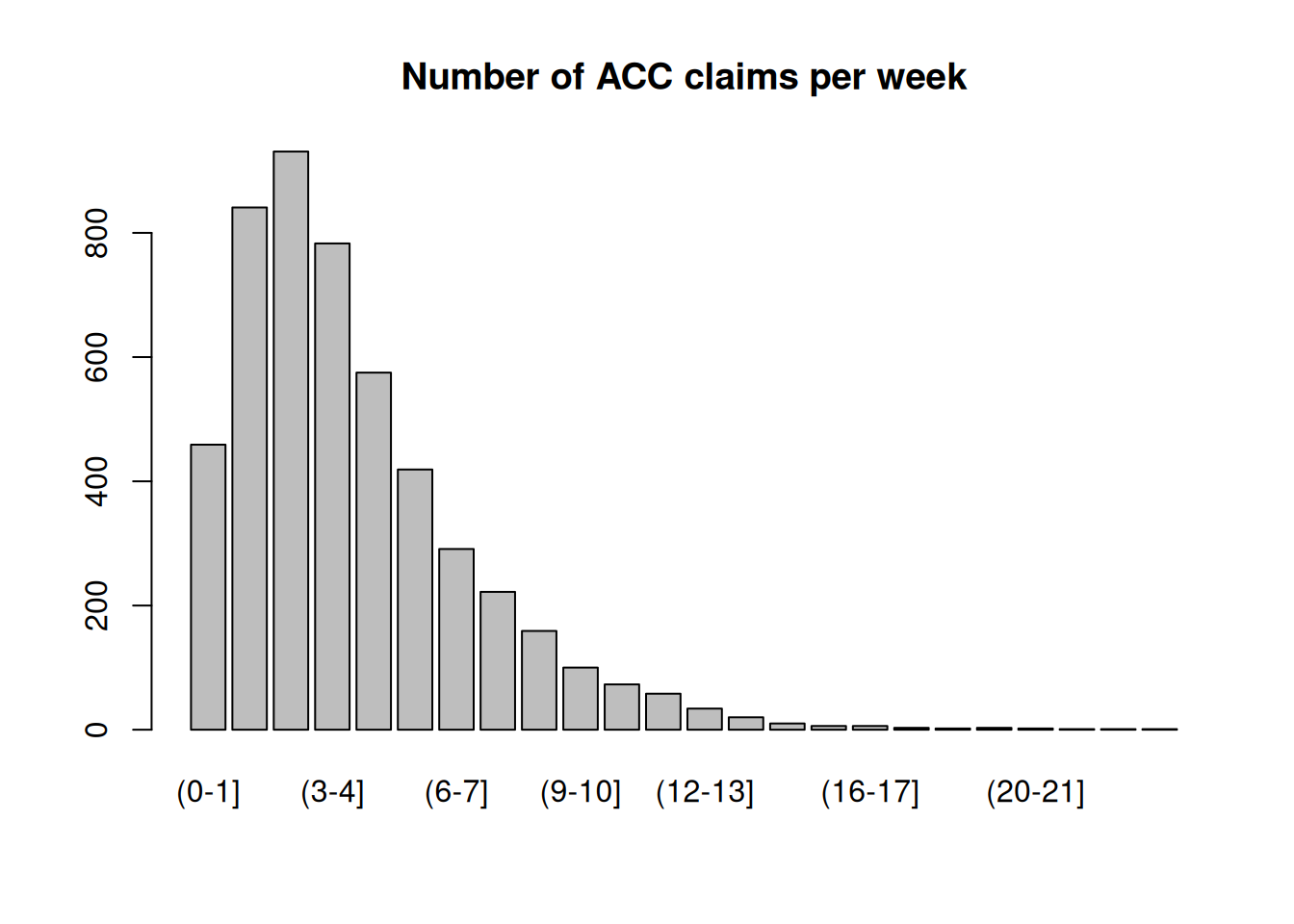
Suppose you wish to estimate the number of days injured people are off work by taking a sample of records: this is our variable of interest \(Y\) . Assume that you have information on the number of ACC claims that employers send in each week: this is your auxiliary information \(X\) which you have for every employer – and we have good reason to expect that \(X\) and \(Y\) are correlated, which means that \(X\) will be a good stratification variable.
Suppose that you wish to form four strata. The Table 8.1 sets out the necessary data for calculating the stratum boundaries. For each of 5000 companies we know \(X\) , the number of claims that company makes per week, on average. The data are given in Table 8.1.
(Note: These average numbers of claims are decimal values, and \((5,6]\) means the interval 5 to 6 excluding 5 but including 6.)
| \(j\) | No. of ACC claims per week | \(f_j\) | \(\sqrt\) | \(\sum_^j\sqrt\) |
|---|---|---|---|---|
| 1 | (0-1] | 459 | 21.4 | 21.4 |
| 2 | (1-2] | 841 | 29.0 | 50.4 |
| 3 | (2-3] | 931 | 30.5 | 80.9 |
| 4 | (3-4] | 783 | 28.0 | 108.9 |
| 5 | (4-5] | 575 | 24.0 | 132.9 |
| 6 | (5-6] | 419 | 20.5 | 153.4 |
| 7 | (6-7] | 291 | 17.1 | 170.4 |
| 8 | (7-8] | 222 | 14.9 | 185.3 |
| 9 | (8-9] | 159 | 12.6 | 197.9 |
| 10 | (9-10] | 100 | 10.0 | 207.9 |
| 11 | (10-11] | 73 | 8.5 | 216.5 |
| 12 | (11-12] | 58 | 7.6 | 224.1 |
| 13 | (12-13] | 34 | 5.8 | 229.9 |
| 14 | (13-14] | 20 | 4.5 | 234.4 |
| 15 | (14-15] | 10 | 3.2 | 237.6 |
| 16 | (15-16] | 6 | 2.4 | 240.0 |
| 17 | (16-17] | 6 | 2.4 | 242.5 |
| 18 | (17-18] | 3 | 1.7 | 244.2 |
| 19 | (18-19] | 2 | 1.4 | 245.6 |
| 20 | (19-20] | 3 | 1.7 | 247.3 |
| 21 | (20-21] | 2 | 1.4 | 248.8 |
| 22 | (21-22] | 1 | 1.0 | 249.8 |
| 23 | (22-23] | 1 | 1.0 | 250.8 |
| 24 | (23-24] | 1 | 1.0 | 251.8 |

Figure 8.1: ACC Claims Distribution
Since \(\sum_^\sqrt(y)>= 251.8 \approx 252\) and we want \(H=4\) strata, the interval boundaries on the cumulative \(\sqrt\) scale are \(252/4, 2 \times 252/4, 3 \times 252/4\) , i.e. \(63, 126, 189\) . The actual cumulative \(\sqrt\) numbers nearest these are: \(50.4, 132.9, 185.3\) , so that the interval boundaries on the \(f\) scale are \(2, 5, 8\) : i.e 1-2 claims a week, 4-5 claims a week, and 7-8 claims a week. Therefore the four strata we form are \((0,2], (2,5], (5,8], (8,24]\) .
Where we have access to detailed information from a previous Census, with the advent of powerful computers, it is conceivable to consider tackling this problem as one of minimizing the variance of the stratified estimator subject to some constraints such as stratum size, etc. Also in practice when we survey we don’t collect just one variable. This means that it is very likely that different variables may require different stratifications, which is not practicable. Hence we need to find compromise stratifications and this is only practical by using computers.
Alternatively, we can consider applying multivariate classification methods to form homogeneous groups within the population which will become our strata, or building blocks for them. Such methods appeal to infinite population models and hence may seem subject to criticisms about the reasonableness of such models. However, having formed the strata, under classical finite population sampling the inferential framework comes from the randomization of the independent samples and not any models used to form the strata. So our inference is still somewhat assumption free.
Moreover, whatever statistical methods we use for forming strata, our aim is to form strata which are robust to changes in the population. Hence we shouldn’t blindly optimize our design on historic data.
Once the strata have been defined we have a total sample size \(n\) , which we want to allocate to each stratum in proportions \(p_h\) , so that the proportion of the sample allocated to stratum \(h\) is \[\begin p_h = \frac \end\] and \[\begin \sum_^H p_h=1 \end\] If we know the allocation proportions \(p_h\) and the sample size \(n\) then the number allocated to stratum \(h\) is the nearest integer to: \[ n_h = p_h n \]
There are several methods for allocating the sample. Some of these are:
This is also called a self weighting design because the weights are the same for all sample members, no matter which stratum: \[ w_h = \frac = N_h\frac = \frac \] which are the same weights we’d get if we took a SRSWOR. (However the design still needs to be analysed using the Stratified SRS formulae.)
In a survey of students, 100 students are to be allocated across two strata: undergraduate and postgraduate. It costs twice as much to survey a postgraduate as an undergraduate, and the standard deviation of age (a key design variable) is three times higher amongst postgraduates than among undergraduates. 20% of the student body are postgraduates.
Allocate these 100 students across the two strata using each of the following methods:
There are \(H=2\) strata. The information we have is
| \(h\) | Stratum | Stratum Fraction \(F_h\) | Cost, \(c_h\) | Std. Dev. \(S_h\) |
|---|---|---|---|---|
| 1 | Undergraduate | 0.80 | \(C\) | \(S\) |
| 2 | Postgraduate | 0.20 | \(2C\) | \(3S\) |
Note that for these calculations we don’t actually have to know the value of the undergraduate cost \(C\) , or the standard deviation of undergraduate age \(S\) : just their relative sizes.
We have \(n=100\) students to allocate.
| \(h\) | Stratum | \(p_h\) | \(n_h=np_h\) | Cost, \(n_hc_h\) |
|---|---|---|---|---|
| 1 | Undergraduate | 0.50 | 50 | \(50\times C=50C\) |
| 2 | Postgraduate | 0.50 | 50 | \(50\times 2C=100C\) |
| Total | 1.00 | 100 | \(150C\) |
| \(h\) | Stratum | \(p_h\) | \(n_h=np_h\) | Cost, \(n_hc_h\) |
|---|---|---|---|---|
| 1 | Undergraduate | 0.80 | 80 | \(80\times C=80C\) |
| 2 | Postgraduate | 0.20 | 20 | \(20\times 2C=40C\) |
| Total | 1.00 | 100 | \(120C\) |
| \(h\) | Stratum | \(F_hS_h\) | \(p_h=F_hS_h/\sum_k F_kS_k\) | \(n_h=np_h\) | Cost, \(n_hc_h\) |
|---|---|---|---|---|---|
| 1 | Undergraduate | \((0.8)(S) = 0.8S\) | \(0.8S/1.4S = 0.57\) | 57 | \(57\times C=57C\) |
| 2 | Postgraduate | \((0.2)(3S) = 0.6S\) | \(0.6S/1.4S = 0.43\) | 43 | \(43\times 2C=86C\) |
| Total | \(1.4S\) | 1.00 | 100 | \(143C\) |
| \(h\) | Stratum | \(F_hS_h/\sqrt\) | \(p_h \propto F_hS_h/\sqrt\) | \(n_h=np_h\) | Cost, \(n_hc_h\) |
|---|---|---|---|---|---|
| 1 | Undergraduate | \((0.8)(S)/\sqrt = 0.80S/\sqrt\) | \(0.80/1.22 = 0.66\) | 66 | \(66\times C=66C\) |
| 2 | Postgraduate | \((0.2)(3S)/\sqrt = 0.42S/\sqrt\) | \(0.42/1.22 = 0.34\) | 34 | \(34\times 2C=68C\) |
| Total | \(1.22S/\sqrt\) | 1.00 | 100 | \(134C\) |
Total costs are \[ \text = n_1C_1 + n_2C_2 = n_1C + n_22C = (n_1+2n_2)C \]
Relative costs, compared to Equal allocation:
| Method | Allocation | Total Cost | Relative Cost |
|---|---|---|---|
| Equal | (50,50) | \(150C\) | 1.00 |
| Proportional | (80,20) | \(120C\) | 0.80 |
| Neyman | (57,43) | \(143C\) | 0.95 |
| Optimal | (66,34) | \(134C\) | 0.89 |
At fixed sample size, Neyman allocation is always best. It is 5% cheaper than equal allocation. Proportional allocation is the cheapest, but not the most efficient.
Table 8.2 displays the difference between Proportional and Neyman Allocation for the ACC data and the four strata chosen by the cumulative \(\sqrt\) rule.
| Stratum | Size | Std. Dev | Fraction | Equal | Proportional | Neyman | |
|---|---|---|---|---|---|---|---|
| \(h\) | \(N_h\) | \(S_h\) | \(F_h\) | \(N_hS_h\) | \(p_h=\frac\) | \(p_h=F_h\) | \(p_h=\frac\) |
| 1 | 1300 | 0.496 | 0.496 | 644.8 | 0.25 | 0.26 | 0.14 |
| 2 | 2289 | 0.853 | 0.853 | 1952.5 | 0.25 | 0.46 | 0.43 |
| 3 | 932 | 0.852 | 0.852 | 794.1 | 0.25 | 0.19 | 0.17 |
| 4 | 479 | 2.441 | 2.441 | 1169.2 | 0.25 | 0.10 | 0.26 |
| Total | 5000 | 1.000 | 4560.6 | 1.00 | 1.00 | 1.00 |
Note that \(\bfa>_>\) can be greater than \(\bfa>_>\) if the variability between strata is less than the variability within strata.
Note also that this decomposition of variance shows that a stratified SRS sample design is more efficient than an SRS sample design. With a good choice of stratification, the design effect of stratified SRS under Neyman or optimal allocation is often considerably less than 1.
In general in the allocation of a total sample of size \(n\) across strata we can write \[ n_h = p_hn \] where \(p_h\) is the proportion of the sample allocated to stratum \(h\) , and \(\sum_hp_h=1\) .
Now assume that we want a particular standard error of an estimate of the total \(\bfa>\) . So we can write \[\begin \bfa> &=& \bfa>^2\\ &=& \sum_^H N_h^2 \left(1-\frac\right)\frac\\ &=& \sum_^H N_h^2 \left(1-\frac\right)\frac\\ &=& \frac\sum_^H \frac - \sum_^HN_hS_h^2 \end\] which can be rearranged to \[\begin n = \frac<\sum_^H \frac>< \bfa>^2 + \sum_^HN_hS_h^2> \end\] This expression is particularly simple for proportional allocation where \[ p_h = \frac \] in which case \[\begin n = \frac
Note that strata may be used in a sample design not so much to control the variance, but to control the sample size in subpopulations. If that is the case it is best to calculate the minimum sample size required separately for each stratum, based on a required standard error for each stratum.